Beginning Complexity - Resilience Engineering

This year I’ve been exploring the field of Resilience Engineering. Resilience Engineering is concerned with building complex systems that are resilient to change and disruption. I’m interested in how we can understand and reason with complex systems. Here I write what I’ve learned so far, and how we can apply it. Most of the ideas I discuss here are proposed by Dr Richard Cook, John Allspaw, and Prof David D. Woods.

A system is made up of a networked group of actors. Each can communicate with other actors, and there may be many instances of the same actor running within the system. Let’s use a hypothetical accounting SaaS as the example of a system. We can imagine the amount of technology that goes into building this. There are web services running in different containerisation and virtualisation platforms. Sharded databases with automatic failover built in, caches, queues, event systems, file storage, mobile apps, logging, monitoring, alerting. The list goes on. On the face of it the system is complicated enough, but there’s much more going on.

There’s a false premise that an IT system is made purely of technology. This is what engineers strive for. We’d like to think that by implementing the correct architecture, design patterns, and testing strategies we could have an IT system running without us needing to intervene. We could imagine sometimes having to step into the system for tasks like adding new features, scaling it, or fixing it. This might be true for small, stateless, command line applications. But not for complex IT systems.

All systems require humans to operate.

When we think of how we’re involved in system operations, incident response is the first thing that springs to mind. This covers outages, bugs, and unexpected behaviour of the system. Not all cause harm to the organisation, but those that do are the ones we remember.

Incidents aside, we do a lot of proactive work to keep systems running:

• Checking monitoring dashboards and logs to confirm the system is operating.
• Upgrading libraries.
• Software deployments for maintenance tasks such as rotating API keys.
• Changing the value on a feature flag.
• Helping people use the system through customer support.
• Helping people build and interact with the system, internal Slack.

Think of other ‘business as usual’ tasks at different levels of abstraction. The owners of the database may do a transparent failover in order to upgrade and reboot a host. A technician in the data centre may be swapping out a failed drive in the RAID array. These events could all happen simultaneously, and the system would continue to operate. If never done, these proactive tasks will eventually cause outages to the system.

“It’s not surprising that your system sometimes fails. What is surprising is that it ever worked at all” - Dr Richard Cook

Our business as usual work is what keeps systems running. The IT system is made of the technology (code, databases, etc), and the people who operate it.

The distinction between these 2 terms is important.

Complicated tasks are typically deterministic. We can understand it and carry it out by following a specific set of steps. Usually in the form of best practices or documentation. For example assembling flat pack furniture, or writing a sorting algorithm. Complicated tasks are generally mechanical by nature. They may be difficult to understand, but can be learned. Some complicated tasks can be verified through testing.

Complex tasks are non-deterministic. We may think we know how it works, or think we know the principles behind how it works, but in reality we don’t. We trick ourselves into thinking they are just complicated with thoughts like “If only I had more information then I could understand this”. Some examples of complex systems are weather forecasting and an accounting SaaS. Even if we understand some parts of the system, emergent behaviour can arise which often surprises us. We can never understand complex systems.

If we can never understand complex systems how do we reason about how they operate? Dr Richard Cook presents this model.

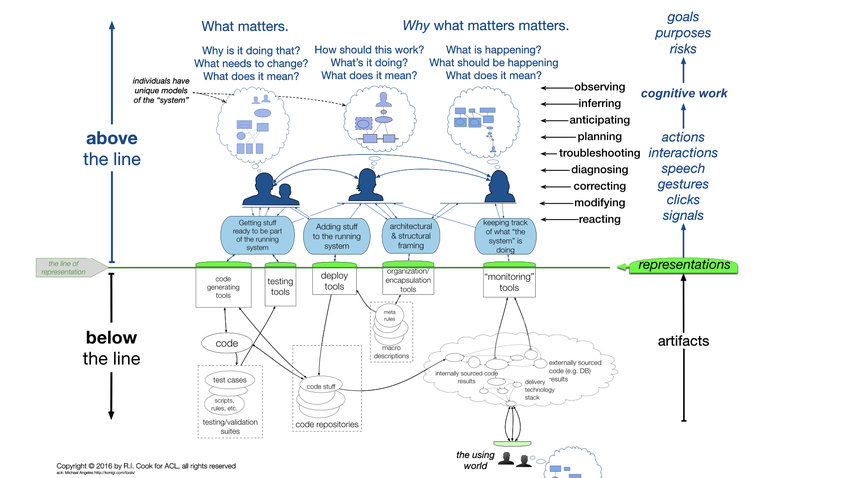
Below the line is the executable code, bits on the network, deployment tools, and silicon we tricked into performing computations. What is below the line cannot be examined. It’s just shadows on a cave wall.

The line of representation is how we interact with what’s below the line. It’s an abstraction in the form of dashboards, monitoring tools, log output and SSH sessions.

We, the people involved in the system, are above the line. Each of us form mental models of how the system operates. Remember that the system is both technical and social so our mental model includes both. The code we write, documentation we read, and data from the tools in the line of representation influence the technical side of our mental model. The people we talk to, discussions we have, and understanding of what each other do forms the social side of the mental model.

We use this mental model of the system everywhere: to plan new development work, debug a problem, or respond to incidents. When the system surprises us it’s not because what was below the line was ‘wrong’. It’s because our mental model of how the system works was incorrect. So it’s vital that we, as individuals and an organisation, continually learn, develop, and share evermore accurate mental models of the system.

Chaos Engineering is a technique where we proactively test the real behaviour of the system. Using our mental model of the system we make a hypothesis, eg. if latency between our web service and the database increased, then we expect the web service to continue to operate with a slower response time and alert X to fire. We then run this scenario on the actual system, and incorporate any learnings into our mental model.

Learning from Incidents is a way to retrospectively learn from past behaviour. Incidents and outages, which are traditionally dreaded by organisations, are the greatest opportunity to learn about the system. By carrying out effective postmortems, and sharing and discussing learnings, we improve our mental models.

Chaos Engineering and Learning From Incidents reveal signals from ‘below the line’. They’re a rare source of information as to how the system actually operates.

“As the complexity of a system increases, the accuracy of any agent’s model of that system decreases” - David Woods

I find it interesting that our response to incidents is all taking place above the line. Tools in the line of representation show us some abstracted information about the system. We take this information, feed it into our mental model of how the system operates, and attempt to come up with actions which might resolve the issue. An incident gets resolved when a responder’s mental model is close enough to the actual behaviour of the system.

When a system changes the complexity of the system increases. To us, the most obvious changes are code deployments. But the system is more than code. Think how complexity increases when..

• Customers use the system in new or unexpected ways.
• New technology platforms are added to the system. People must recalibrate their mental models to factor this in.
• People in the organisation suddenly change the way they work and communicate (eg. enforced working from home).
• Organisation restructures, change ownership of actors within the system.
• Individuals and teams get overloaded with work. Time people spent refining and sharing their mental model of how the system works is switched to adding complexity to the system.

In one of his talks Cook remarked that the age of thinking that the majority of incidents are directly caused by deployments is over. Safer development and delivery practices such as enforced test coverage, code review, feature flagging, blue/green deployments, and small regular releases do a good job at reducing errors local to that code base. In that talk Cook mentions “less than half of the incidents we see are related to the last deploy”. I couldn’t find any data for this claim, take a look and see what it is in the systems you operate it.

The default behaviour of any complex system is failure. It’s intrinsic. You get it for free when you build any system, and it gets worse when the system becomes more complex.

“You build things differently when you expect them to fail” - Cook

We should strive to reduce and isolate complexity in the system, but must acknowledge the system will always remain complex. Once we’ve recognised that complexity exists we can then start adapting to it. This quote from the STELLA report sums it up well (my highlight).

Resilience in business-critical software is derived from the capabilities of the workers and from the deliberate configuration of the platforms, the workspace, and the organisation so that those people can do this work. It is adaptability that allows successful responses to anomalies and successful grasping of new opportunities. The organisational and technical structures of the enterprise are intentionally configured to generate and sustain the enterprise’s adaptive capacity. In a complex, uncertain world where no individual can have an accurate model of the system, it is adaptive capacity that distinguishes the successful.

• Above the Line, Below the Line - Dr Richard Cook
• Working at the Centre of the Cyclone - Dr Richard Cook
• How Complex Systems Fail - Dr Richard Cook
• STELLA Report - David Woods & SNAFU Catchers
• Principles of Chaos Engineering
• Innumberable conversations with @PGSchuermann